The physics (and mathematics) of gravitational microlensing
Gravitational microlensing is understood as the transient brightening
of an observed star
resulting from the gravitational bending of its light by an intervening foreground 'lens' star.
The underlying physics is remarkably simple.
The deflection
- increases with the mass of the lens star (proportionally), and
- decreases with the separation of the light ray from the lens
star (inversely proportionally).
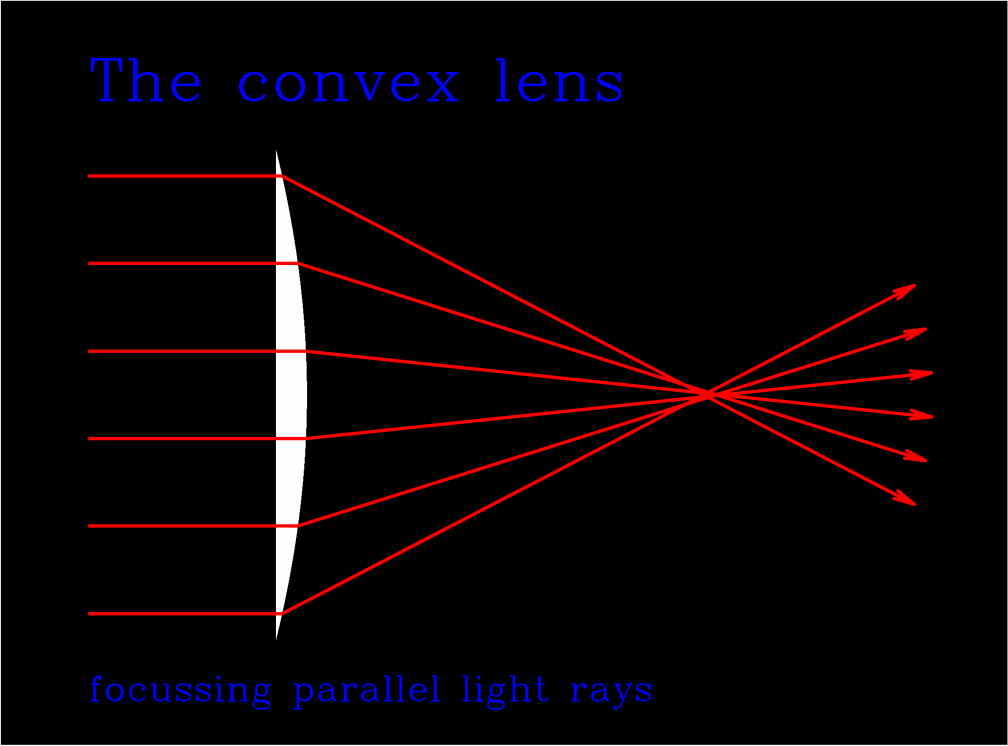
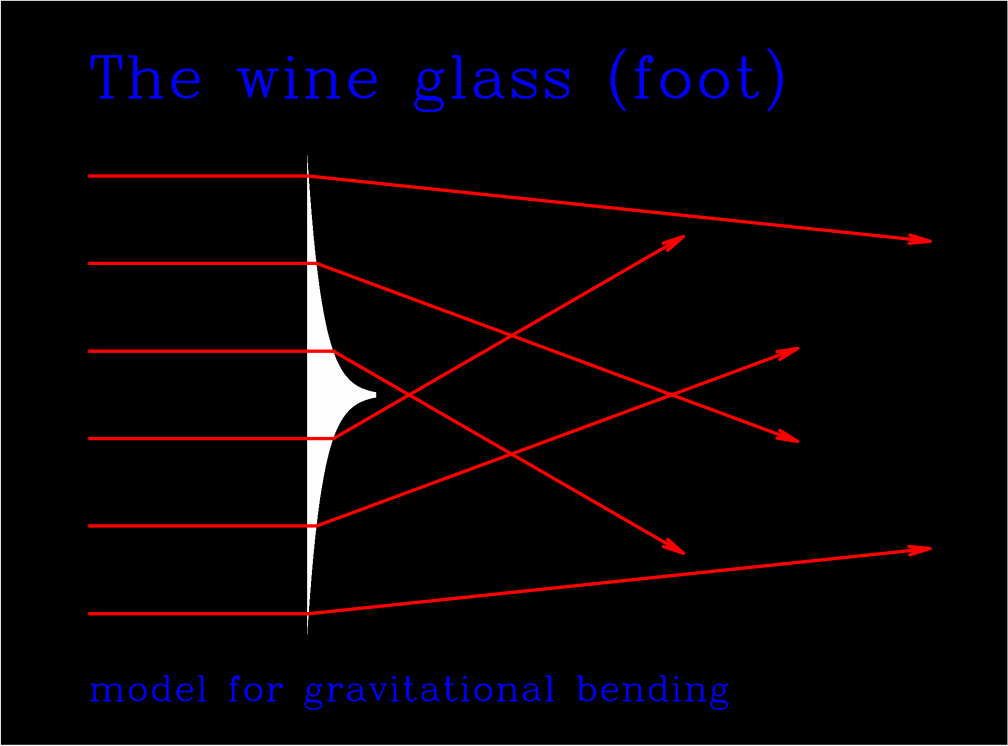
The gravitational bending of light thereby differs significantly from the effect caused by an optical convex lens, but is rather
similar to the deflection by a glass body in the shape of the foot of a
wine glass.
Deflection of parallel light rays by a convex lens and by the foot of
the wine glass, which represents an analogy to the gravitational bending
of light. With the deflection decreasing towards its centre, the
convex lens leads to a focussing. A different behaviour results for
the light bending by massive bodies, where the deflection angle increases
the closer the light ray approaches.
Explicitly, for a lens of mass M, the deflection law for a light
ray at an impact separation &xi reads
where G denotes the universal gravitational constant, and
c is the vacuum speed of light. This amount, as predicted by Einstein's theory of General
Relativity, is in fact exactly twice the Newtonian value. This factor
of two is however the only relevant contribution of General Relativity
to the physics of gravitational microlensing.
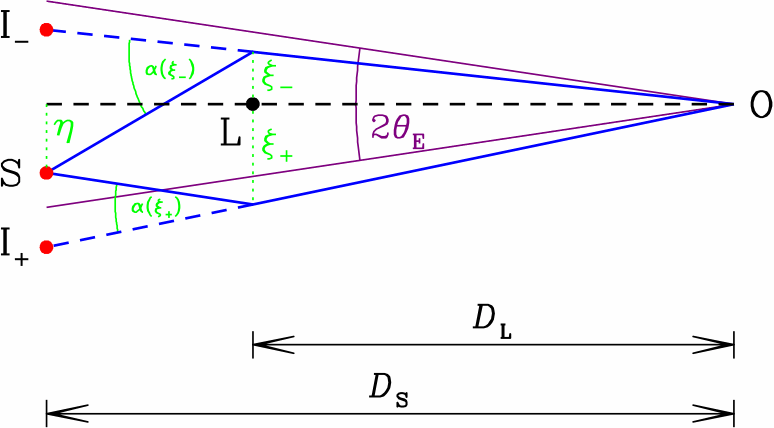
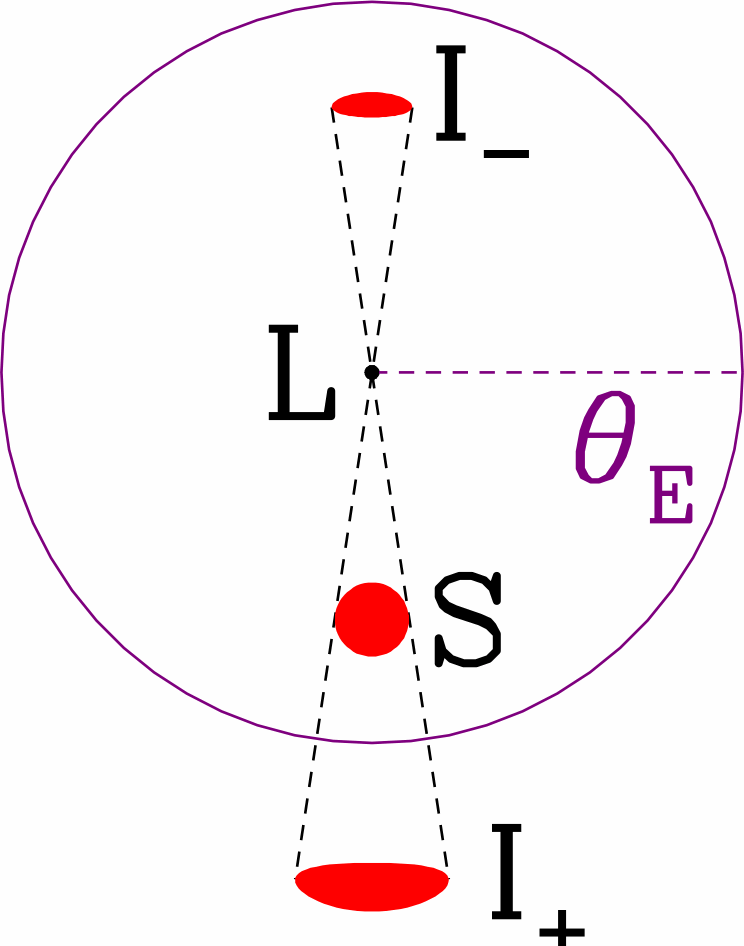
Side view (left) and observer's view (right) on a source star (S) affected
by gravitational microlensing due to a foreground lens star (L), where
two possible light paths to the observer (O) correspond to two apparent images I- and
I+.
As found by Einstein as early as 1912, geometry demands
a ray-tracing equation resulting from the condition that light rays
originating from the source star hit the observer. It provides the
separation η of the light ray from the optical
axis connecting lens star and observer as the light leaves the source
at distance DS as a function of ξ,
the separation of the light ray from the lens star at distance DL as
First two pages of the discussion of gravitational microlensing in
Einstein's notebook of 1912. © The Einstein Archives
Einstein also discovered that there is a unique characteristic scale,
now called the angular Einstein radius θE, that absorbs all the
physical parameters, namely the mass M of the lens star, as
well as the lens and source distances DL and
DS:
With dimensionless
angular coordinates
the ray-tracing equation takes the simple form
This leads to a quadratic equation for the image positions x as
function of the true source coordinate y, whose two solutions
read
It can easily be verified that one of the two images always falls inside
the angular Einstein radius (|x−| < 1), while the other one
is always to be found outside (|x+| > 1), unless lens and source star are perfectly aligned (y = 0), in which case a ring-like image (Einstein ring) results, whose
angular radius is equal to θE (given that x = 1).
Apart from the images appearing at angular positions different from that
of the source star, gravitational lensing also accounts for a distortion, where
the images are stretched radially by dx/dy and tangentially by x/y (given that the polar angle is conserved). Since this changes
the solid angle from which light of the source star is received at the
observer, a combined
magnification A(y) of both images, given by
is being observed, whereas the images themselves cannot be resolved
by current optical telescopes, given that their separation is less
than a milli-arcsecond.
While the source star always happens to be magnified (A > 1),
and never de-magnified, the magnification is the larger the more closely
source and lens star are aligned. Therefore,
if stars can be assumed to move uniformly, microlensing light curves
are symmetric with respect to a peak, which is reached at the
epoch that marks the minimal angular impact between lens and source
star.
back
Martin Dominik, 25 May 2008